2020. 8. 15. 12:46ㆍAlgorithm/알고리즘 이론 정리
정렬 문제를 Convex Hull 문제로 환원하는 방법을 소개합니다.
Convex Hull 문제를 정렬 문제로 환원할 수 있다는 것은 널리 알려져 있는 사실이다.
Graham Scan알고리즘은 점들을 각도 순으로 정렬한 뒤 한 번의 스캔을 통해 Convex Hull을 구하는 알고리즘이기 때문이다.
곧, 다항 시간 내에 Convex Hull 문제를 점들을 정렬하는 문제로 환원할 수 있다.
여기서는 정렬 후에 이루어지는 스캔 (O(N))이 변환 시간이 된다.
다음과 같이 나타낸다.

여기까지는 Convex Hull과 다항식 시간 변환의 개념을 안다면 누구나 알 수 있는 사실이다.
한 발 더 나아가보자.
정렬 문제를 Convex Hull을 구하는 문제로 변환할 수 있을까?
즉, Convex Hull을 구하는 알고리즘을 알고 있을 때 원하는 수들을 정렬할 수 있는가?
혹자는 Convex Hull을 구할 때 정렬을 사용하므로 이는 모순적이다고 주장할 수 있다. 그렇지만 이는 Convex Hull을 구하는 방법에는 여러가지가 있는 것을 간과한 것이다. 우리는 Convex Hull을 구하는 문제를 변환하는 것이므로 정렬을 사용하지 않는 알고리즘을 택할 수 있다.
어떻게 정렬 문제를 Convex Hull 알고리즘을 이용하여 해결할까?
주어진 N개의 실수 x_1,x_2,...,x_N를 정렬하는 문제를 푼다고 생각해보자.
각각의 수를 x좌표로 하는 y = x*x 위의 점들을 표시한다.
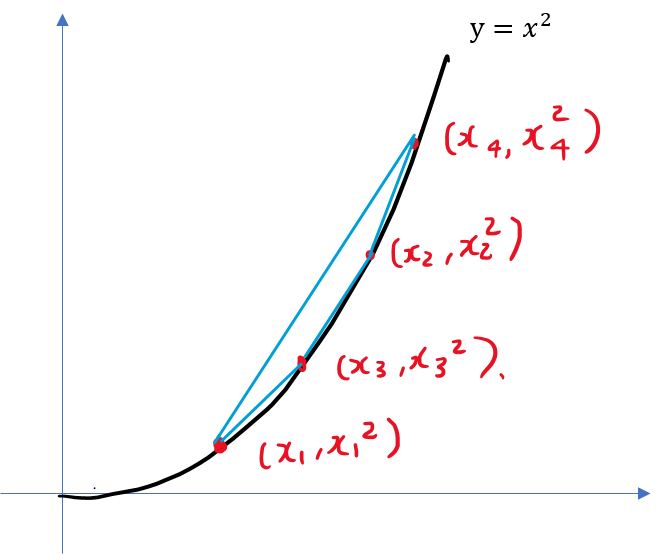
y=x*x는 이계도함수가 2이고 항상 양수이다. 즉, 이 그래프는 Concave Up <=> Convex Down이다.
이 그래프 위의 점들에 대하여 Convex Hull을 구하면 모든 점들이 그 Convex Hull에 속한다.
이때 짚고 넘어갈 것은 Convex Hull을 구한다는 것은 하나의 볼록 다각형을 구하는 것을 의미한다. 다각형은 점들 간의 순서가 명확하다. 시계/반시계 방향으로 점들이 구해질테지만, 편의상 반시계 방향으로 점들을 구한다고 하자.
만약 우리가 y=x^2 위 점들의 Convex Hull을 구할 수 있다면 반시계 방향으로 점들을 나열할 수 있음을 의미하고, 그 순서에 따라 각각의 x좌표를 나열한다.
정렬이 완료되었다.
따라서 정렬 문제를 Convex Hull 문제로 변환할 수 있다.
오늘 우리가 배운 것은?
Convex Hull 문제와 정렬 문제는 양방향 다항식 시간 변환이 가능하다.
아이디어 : Stack Overflow, Ícaro Dourado
https://stackoverflow.com/questions/13597392/using-convex-hull-algorithm-to-sort-integers
'Algorithm > 알고리즘 이론 정리' 카테고리의 다른 글
| BFS 메모리 줄이는 방법 (0) | 2020.11.18 |
|---|---|
| Li Chao Tree 공부 (0) | 2020.11.14 |
| Knuth Optimization (0) | 2020.11.12 |
| 모든 Mother Vertex를 O(V+E)에 구하는 알고리즘 (0) | 2020.09.25 |
| 특정 조건에서 LCS를 O((n+m) log (nm))에 구하는 알고리즘 (0) | 2020.09.25 |